[SNN Basic Tutorial 4] SNN을 위한 회로이론(2): RC회로
SNN Basic Tutorial 목차
지난 글에서는 회로 이해에 필요한 기초적인 내용을 살펴보았습니다. 이번 글에서는 이전 내용을 기반으로 RC회로에 대하여 다뤄보도록 하겠습니다.
이번 글은 수식이 많지만, 천천히, 차례차례 읽고 이해하다 보면 어느새 이번 글의 목적인 RC회로의 응답을 구할 수 있으실 겁니다.
RC 회로란?
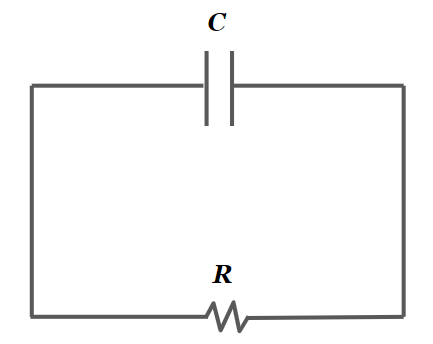
RC회로란 아래 그림과 같이 저항(R)과 커페시터(C)로 이루어진 회로를 말합니다. RC회로는 저장요소인 커페시터가 하나 있는 구조로써 1차회로 중 하나이며, 또 다른 1차회로로는 저항과 하나의 인덕터로 이루어진 RC회로가 있습니다. 회로이론에서는 미분방정식을 이용하여 1차회로의 저장요소에 흐르는 전압 혹은 전류를 찾는 방법을 배웁니다.
이번 글에서는 RC회로에 흐르는 전압응답을 구하는 방법을 알아볼 것입니다. 다른 말로는 RC회로의 전압을 시간에 따른 수식으로 구하는 방법을 알아볼 것입니다. RC회로의 전압응답을 구하는 것은 추후 SNN을 이해하는데 필수적인데, SNN의 가장 기초적인 모델인 Leaky Integrate and Fire(LIF) 모델의 기초가 되는 회로가 바로 이 RC회로이기 때문입니다. 때문에 RC회로의 전압응답을 구할 수 있다면, 시간에 따른 LIF 뉴런 모델의 membrane potential 또한 구할 수 있습니다. 저 또한 RC회로를 공부하면서 그동안 어려웠던 SNN 자료들을 훨씬 더 쉽게 이해할 수 있었습니다. 때문에 RC회로가 낮설다면 이 글을 읽어보신 후에 다음 글로 넘어가시기를 추천드립니다.
RC회로의 완전응답
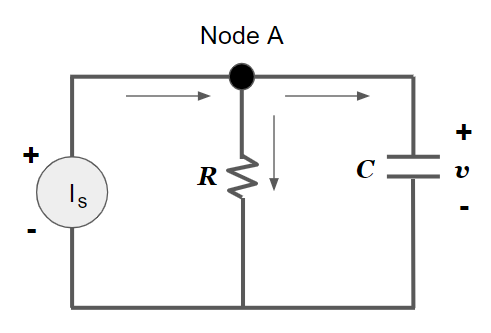
이 글에서 저희가 최종적으로 전압응답을 구하고자 하는 회로는 위 그림처럼 저항과 커페시터만 연결되어있는 회로가 아닌, DC전압원이 추가적으로 부착되어있는 RC회로입니다(DC전압원은 전류, 전압 모두 일정한 출력을 내줍니다). DC전압원이 있는 RC회로의 형태는 아래와 같습니다:
이 회로에는 전력을 생성해내는 소자가 2개 있습니다. 하나는 $I_S$로 표기되는 DC전압원으로, 인위적으로 일정한 전력을 생성해내기에 강제응답이라고 부릅니다. 하나는 커페시터 $C$로, 커페시터에 저장된 전력이 회로를 타고 흐르게 됩니다. 이는 인위적인 공급이 아닌 커페시터에 저장된 전력이 자연스럽게 흐른다는 관점에서 비롯하여 고유응답이라고 부릅니다. 회로의 최종적인 응답(완전응답)은 강제응답과 고유응답의 합으로 구해집니다. 이번 글에서는 RC회로의 고유응답과 강제응답을 각각 유도해보고 두 식을 더하여 완전응답까지 구해보도록 하겠습니다.
고유응답 유도: 무공급원 RC회로
무공급원 RC회로란 별도의 전원부가 없는 RC회로를 말합니다. 무공급원 RC회로가 가능한 이유는 커페시터가 전력을 저장할 수 있기 때문인데, 때문에 무공급원 RC회로를 이야기할 때는 커페시터가(전원부 역할을 할 수 있도록) 충전되어있는 상태를 가정합니다. 이번 글에서는 시간 $t$에 따른 무공급원 RC회로의 전압을 구할 수 있는 방법을 알아보겠습니다.
위 그림에서 Node A 기준으로 봤을 때, KCL에 의하여 전원부로부터 Node A로 들어오는 전류 $I_S$ 의 크기는 커페시터 $C$와 저항 $R$로 흐르는 전류$I_C$, $I_R$의 합과 같습니다.
\[I_S = I_C + I_R\]위 RC회로 그림에서 전원부로부터 공급받는 전류가 0일 때를 무공급원 RC회로로 볼 수 있으며, 따라서 다음과 같은 식이 됩니다:
\[I_C + I_R = 0\]위 식에 옴의 법칙을 적용하여 저희가 원하는 형태가 되도록 전개해보겠습니다. 전원부가 없다고 가정하므로 아래 식에서 고려되는 전압 $v_C$ 혹은 $v_C(t)$는 충전된 커페시터의 전압을 뜻합니다.
\[C\frac{dv_C}{dt}+\frac{v_C}{R} = 0\] \[\frac{dv_C}{dt}=-\frac{v_C}{RC}\] \[\frac{dv_C}{v_C} = -\frac{dt}{RC}\]전개된 식의 양 변을 적분하면 다음과 같습니다($K$는 적분상수):
\[\int{\frac{dv_C}{v_C}}=-\int{\frac{dt}{RC}}\] \[\ln(v_C) = -\frac{1}{RC}\int{1\cdot dt} = -\frac{t}{RC} + K\] \[\ln(v_C) =-\frac{t}{RC} + K\] \[v_C(t) = e^{-\frac{t}{RC}+K} = e^{K}e^{-\frac{t}{RC}}\]위 식에서 지수가 적분상수 $K$인 자연상수$e^K$는 큰 의미가 없으므로 $K$로 대체해줍니다:
\[\therefore v_C(t) = Ke^{-\frac{t}{RC}}\]만약 공급원이 없이 저항과 커페시터만 있는 RC회로라면, 위 공식에 $t=0$을 넣어 식의 초기값 $v_C(0)$을 구할 수 있습니다:
\[v_C(0) = Ke^{-\frac{0}{RC}} = K \cdot 1 = K\] \[v_C(t) = v_C(0) \cdot e^{-\frac{t}{RC}}\]강제응답 유도
이번에는 공급원이 작동하는 RC회로의 전압 응답을 구해보겠습니다. 먼저 RC회로에 KCL 법칙을 적용해 유도한 공식을 적어놓고 시작하겠습니다. 아래 식에서 고려되는 전압 $v_S$ 혹은 $v_S(t)$는 전압원의 전압입니다(커페시터의 전압이었던 고유응답과의 차이에 유의하시기 바랍니다).
\[C\frac{dv_S}{dt}+\frac{v_S}{R} = I_S\] \[\frac{dv_S}{dt} + \frac{v_S}{RC} = \frac{I_S}{C}\]위 RC회로의 공급원은 DC이기에 전압원의 전압값이 변하지 않으므로, 식에서의 $v_S$값을 변수가 아닌 상수 $A$로 치환할 수 있습니다:
\[\frac{d}{dt}A + \frac{A}{RC} = \frac{I_S}{C}\]위 식의 첫번쨰 항 $\frac{d}{dt}A$는 상수 A를 $t$에 대해 미분하는 형태이므로 소거됩니다 따라서
\[\frac{A}{RC} = \frac{I_S}{C}\] \[A = \frac{I_S}{C} \cdot RC = I_SR = v_S\] \[\therefore v_S = I_SR\]완전응답 유도
위 그림과 같은 RC회로의 완전응답은 강제응답과 고유응답의 합과 같다고 하였습니다. 저희가 위에서 구한 결과를 통해 다음과 같은 식을 유도할 수 있습니다:
\[v(t) = v_C(t) + v_S(t)\] \[v(t) = Ke^{-\frac{t}{RC}} + I_SR\]위 식에서 적분상수 K를 구하면 식이 완성됩니다. 적분상수 K는 다음과 같이 유도할 수 있습니다:
\[v(0) = Ke^{-\frac{0}{RC}} + I_SR = K \cdot 1 + I_SR = K + I_SR\] \[v(0) = K + I_SR\] \[K = v(0) - I_SR\]다음과 같이 구한 K를 완전응답 식에 대입해줌으로써 완전응답을 구할 수 있습니다:
\[\therefore v(t) = (v(0) - I_SR)e^{-\frac{t}{RC}} + I_SR\]마치며
이번 글에서는 RC회로의 전압응답을 구하는 방법을 알아보았습니다. 다음 글에서는 여태까지 공부했던 배경지식을 활용하여, 마침내 SNN의 가장 기본적인 모델인 Leaky Integrate and Fire 모델에 대하여 알아보도록 하겠습니다.
글을 읽으시며 추가설명이 필요한 부분이나 이해가 어려운 부분, 혹은 오류가 있다면 댓글로 적어주시면 적극반영하도록 하겠습니다. 읽어주셔서 감사합니다.